Είμαστε ίσα μέρη ενός συνόλου...
Ο καθένας μας μια (μοναδική) κλασματική μονάδα!
Στην οικογένεια που μεγαλώνουμε, στην τάξη που είμαστε, στο σχολείο που πάμε, στην ομάδα που συμμετέχουμε, στην κοινότητα (μικρή-μεγάλη) που ζούμε, στον κόσμο που ανήκουμε!
"We 're one, but we 're not the same..." που λέει κι ο Bono με τους U2...!
Μαθηματικά, το σημερινό πιάτο μας...
Κλάσματα (γνήσια και καταχρηστικά, δεκαδικά και ισοδύναμα, ομώνυμα και ετερώνυμα), κλασματικές μονάδες, απλοποίηση, σύγκριση-διάταξη... (Ενότητα 1(γ), κεφάλαια 19-24)
1.α) Μετατρέπω τους μεικτούς αριθμούς σε κλάσματα, όπως στο παράδειγμα:
2 3/5 = 2·5+3 /5 = 13/5 3 1/4 = 4 2/3 = 5 5/6 =
β) Μετατρέπω τα κλάσματα σε μεικτούς αριθμούς, όπως στο παράδειγμα:
23/6 = 3 5/6 22/5 = 19/4 = 32/9 =
2.α) Γράφω τις διαιρέσεις ως κλάσματα:
3 : 8 = 4 : 11 = 12 : 7 = 15 : 15 =
β) Γράφω τους δεκαδικούς αριθμούς ως δεκαδικά κλάσματα:
0,9 = 0,04 = 1,3 = 0,022 =
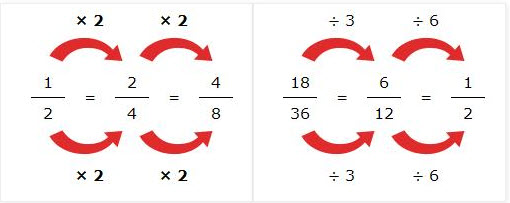
3.α) Συμπληρώνω τα ισοδύναμα κλάσματα:
2/5 = 4/10 = 6/... = ........ = ........ = ......... = ........ = .........
β) Κάνω τα παρακάτω κλάσματα ανάγωγα, όπως στο παράδειγμα:
12/15 = 12:3 / 15:3 = 4/5 15/20 = 18/24 = 32/40 =
4.α) Βάζω τα κλάσματα από το μικρότερο στο μεγαλύτερο (αύξουσα σειρά):
5/7, 8/7, 1/7, 70/7, 3/7, 7/7 →
β) Βάζω τα κλάσματα από το μεγαλύτερο στο μικρότερο (φθίνουσα σειρά):
Σημείωση: Βρίσκω πρώτα ισοδύναμα που να είναι ομώνυμα για να μπορώ να τα συγκρίνω.
5/6, 1/2, 7/9, 11/18, 2/3 →
Ο καθένας μας μια (μοναδική) κλασματική μονάδα!
Στην οικογένεια που μεγαλώνουμε, στην τάξη που είμαστε, στο σχολείο που πάμε, στην ομάδα που συμμετέχουμε, στην κοινότητα (μικρή-μεγάλη) που ζούμε, στον κόσμο που ανήκουμε!
"We 're one, but we 're not the same..." που λέει κι ο Bono με τους U2...!
U2 - "One" (πηγή: YouTube)
Μαθηματικά, το σημερινό πιάτο μας...
Κλάσματα (γνήσια και καταχρηστικά, δεκαδικά και ισοδύναμα, ομώνυμα και ετερώνυμα), κλασματικές μονάδες, απλοποίηση, σύγκριση-διάταξη... (Ενότητα 1(γ), κεφάλαια 19-24)
Ασκήσεις
1.α) Μετατρέπω τους μεικτούς αριθμούς σε κλάσματα, όπως στο παράδειγμα:
2 3/5 = 2·5+3 /5 = 13/5 3 1/4 = 4 2/3 = 5 5/6 =
β) Μετατρέπω τα κλάσματα σε μεικτούς αριθμούς, όπως στο παράδειγμα:
23/6 = 3 5/6 22/5 = 19/4 = 32/9 =
2.α) Γράφω τις διαιρέσεις ως κλάσματα:
3 : 8 = 4 : 11 = 12 : 7 = 15 : 15 =
β) Γράφω τους δεκαδικούς αριθμούς ως δεκαδικά κλάσματα:
0,9 = 0,04 = 1,3 = 0,022 =
3.α) Συμπληρώνω τα ισοδύναμα κλάσματα:
2/5 = 4/10 = 6/... = ........ = ........ = ......... = ........ = .........
β) Κάνω τα παρακάτω κλάσματα ανάγωγα, όπως στο παράδειγμα:
12/15 = 12:3 / 15:3 = 4/5 15/20 = 18/24 = 32/40 =
4.α) Βάζω τα κλάσματα από το μικρότερο στο μεγαλύτερο (αύξουσα σειρά):
5/7, 8/7, 1/7, 70/7, 3/7, 7/7 →
β) Βάζω τα κλάσματα από το μεγαλύτερο στο μικρότερο (φθίνουσα σειρά):
Σημείωση: Βρίσκω πρώτα ισοδύναμα που να είναι ομώνυμα για να μπορώ να τα συγκρίνω.
5/6, 1/2, 7/9, 11/18, 2/3 →
Ισοδύναμα κλάσματα

Πανέμορφες οι φωτογραφίες!
ΑπάντησηΔιαγραφήΚαλησπέρα κύριε καλή εβδομάδα!!!!Ωραίες οι φωτογραφίες από τον δικό μας Μάη!!!!
ΑπάντησηΔιαγραφήΜαριάννα ❤️
Όντως, ό,τι στείλατε ήταν "χάρμα οφθαλμών"...!😊💖
ΑπάντησηΔιαγραφήΚαλή εβδομάδα!!!
ΑπάντησηΔιαγραφήΕλένη
Καλησπέρα σε όλους σας...
ΑπάντησηΔιαγραφήΠαιδιά, να συντομεύουμε λίγο με τις απαντήσεις γιατί έρχεται η επόμενη ανάρτηση. Καλά θα ήταν να τις στείλετε και οι υπόλοιποι ως το βράδυ...
😊😉😍